Application of the Fractional Reduced Differential Transform Method to aTime-Fractional Heat Equation
DOI:
https://doi.org/10.62050/ljsir2025.v3n2.661Keywords:
Anomalous diffusion, FRDTM, FVIM, heat equation, fractional derivativeAbstract
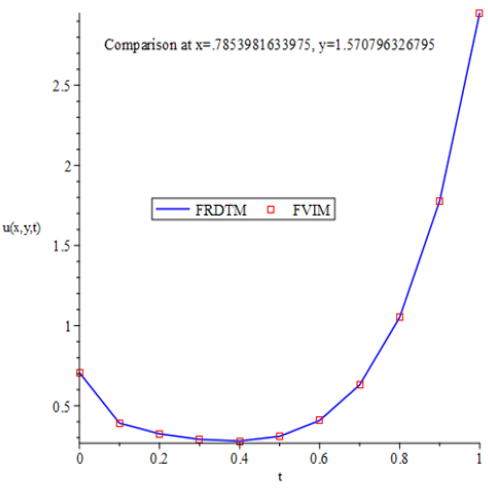
This work deals with the numerical solution of a time-fractional heat equation where a Caputo fractional derivative of order 0 is used in place of the traditional first-order time derivative. This change improves the model's capacity to represent anomalous diffusion behavior and memory effects, which are frequently seen in intricate engineering and physical systems. Applying and evaluating the Fractional Reduced Differential Transform Method (FRDTM) to solve this fractional-order partial differential equation is the aim of this work. The Fractional Variational Iteration Method (FVIM) was used to validate the findings. For different fractional orders, namely, and the classical case where with a known exact solution, two numerical examples were performed. The findings demonstrate that FRDTM offers extremely stable and accurate solutions that closely match the exact solution in the classical case. When it comes to capturing the change from rapid decay at lower fractional orders to more sustained solution profiles as the order increases, the FRDTM performs better than the FVIM. The differences between the two methods demonstrate FRDTM's superior convergence and accuracy across all cases considered. Finally, this study demonstrates the effectiveness of FRDTM as a reliable semi-analytical tool for solving fractional heat problems, and it contributes to advancing computational approaches for solving partial differential equations in science and engineering.
Downloads
References
Gorguis, A., and Benny Chan, W. K. (2008). Heat equation and its comparative solutions. Computers & Mathematics With Applications, 55(12), 2973-2980. https://doi.org/10.1016/j.camwa.2007.11.028
Klages, R., Radons, G. and Sokolov, I.M. (2008). Anomalous Transport, Wiley Online Library.
Evangelista, L.R. and Lenzi, E.K. (2018). Fractional Diffusion Equations and Anomalous Diffusion, Cambridge University Press.
Evans, L. C. (2010). Partial differential equations (2nd ed.). American Mathematical Society.
Metzler, R. and Klafter, J. (2000). The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys Rep. Vol 339(1), Pp.1–77.
Podlubny, I. (1999) fractional differential equations. Academic Press, 8:683-699. https://doi.org/10.1016/j.camwa.2012.01.031
Kilbas, A. A., Srivastava, H. M. and Trujillo, J. J. (2006). Theory and Applications of Fractional Differential. Equations (Elsevier, Netherlands).
Yuste, S. B and Lindenberg, K. (2001). Sub-diffusion-limited A + A reactions. Phys Rev Lett, Vol. 87(11), Pp. 118301.
Chang, A. and Sun, H. (2018). Time-space fractional derivative models for CO 2 transport in heterogeneous media. Fractional Calculus and Applied Analysis, Vol. 21(1), Pp. 151–73.
Ahmad, I., Ali, I., Jan, R., Idris, S. A., and Mousa, M. (2023). Solutions of a three-dimensional multi-term fractional anomalous solute transport model for contamination in groundwater. PLOS ONE, 18(12), e0294348. https://doi.org/10.1371/journal.pone.0294348.
Atay, M. T and Kilic, O. (2013). The semi-analytical solutions for stiff systems of ordinary differential equations by using Variational Iteration Method and Modified Variational Iteration method with comparison to exact solutions. Math Probl Eng. (2013).
Ganjiaw, M. (2010). Solutions of Nonlinear Fractional Differential Equation using Homotopy Analysis Method. Applied Mathematical Modelling, Vol. 33(60), Pp.1634-1641.
Pandey, I., Kumar, S. and Gómez-Aguilar, J.F. (2022). Numerical Solution of the Time Fractional Reaction-advectiondiffusion Equation in Porous Media. Journal of Applied and Computational Mechanics, 8(1), Pp. 84-96.
Odibat, Z. and Momani, S. (2009). The Variational Iteration Method: An Efficient Scheme for Handling Fractional Partial Differential Equations in Fluid Mechanics. Computers & Mathematics with Applications, Vol., 58, Pp. 2199- 2208. http://www.sciencedirect.com/science/article/pii/S0898122109001436
Baleanu, D., Jajarmi, A., Sajjadi, S.S. and Asad, J.H. (2020). The fractional features of a harmonic oscillator with position-dependent mass, Commun. Theor. Phys. 72 (5) (2020) 055002.
Zhang, X. and Yao, L. (2021). Numerical approximation of time-dependent fractional convection-diffusion-wave equation by RBF-FD method. Engineering Analysis with Boundary. Elements, Volume 130, Pp. 1-9.
Bayrak, M.A, Demir, A. and Ozbilge, E. (2020). Numerical solution of fractional diffusion equation by Chebyshev collocation method and residual power series method. Alexandria Engineering Journal, Vol (59), 4709–4717.
Al-rabtah, A. and Abuasad, S. (2023). Effective Modified Fractional Reduced Differential Transform Method for Solving Multi-Term Time-Fractional,Wave-Diffusion Equations. Symmetry, 15(9), 1721. https://doi.org/10.3390/sym15091721.
Kenea, K. S. (2018). Analytic solutions of time-fractional diffusion equations by Fractional Reduced Differential Transform Method (FRDTM). African Journal of Mathematics and Computer Science Research, Vol. 11(2), pp. 14-34. https://doi.org/10.5897/AJMCSR2017.0716.
Arikoglu, A. and Ozkol, I. (2009). Solution of fractional differential equations by using the differential transform method. Chaos, Solitons and Fractals, Vol. 40, Pp. 521–529.
Keskin, Y. and Oturang, G. (2009). Reduced Differential Transform Method for Partial Differential Equations. International Journal of Nonlinear Sciences and Numerical Simulation, 10(6), Pp.741-749.
Ogunfiditimi, F. and Okiotor, N. (2021). Solution of Modified Hirota-Satsuma (MHS) Coupled KdV-Equations by Variational Iteration Method, International Journal of Mathematics Trends and Technology (IJMTT), Vol. 67, No. 5, Pp. 113-125, 2021. https://doi.org/10.14445/22315373/IJMTT-V67I5P514
Wu, G. and Lee, E. (2010). Fractional variational iteration method and its application. Physics Letters A, 374(25), 2506-2509. https://doi.org/10.1016/j.physleta.2010.04.034
Odibat, Z. and Momani, S. (2006). Application of Variational Iteration Method to Nonlinear Differential Equations of Fractional Order. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 70, Pp. 27-34. https://doi.org/10.1515/IJNSNS.2006.7.1.27
Ghosh, U., Sengupta, S., Sarkar, S.and Das, S. (2015). Analytic Solution of Linear Fractional Differential Equation with Jumarie Derivative in Term of Mittag-Leffler Function. American Journal of Mathematical Analysis, Vol. 3, no.2, Pp. 32-38. https://doi.org/10.12691/ajma-3-2-2
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Franklin Olusodayo Ogunfiditimi, Blessing Omojo Akogwu (Author)

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.









