The Health Economics of Life Expectancy
Counting the Days before the Individual’s Roll Call
DOI:
https://doi.org/10.62050/ljsir2025.v3n1.352Keywords:
expectancy, integral, mortality, parsimoniousAbstract
For a life office, the potential deviations from the mortality assumptions applied in premium setting at the time of incepting contracts represents serious threats to its financial performance when underwriting life insurance policies including annuities. Furthermore, in view of the uncertainties associated with the complete expectation of life evolving from the inadequately modelled life expectancy as a form of mortality risk indicator, this study explores the CMI’s generalized Makeham’s mortality law which would be advantageous to compute complete life expectancies. When continuous parsimonious parametric mortality intensities are Makehamized, then the limiting value of the continuous whole life annuity function is construed to mean the complete life expectancy which is expressed in line with special functions such as incomplete upper gamma function for a homogeneous insured population. In this study, the objective are to (i) construct actuarial estimation of individual’s time remaining through single life parameterization from GM(1,2) (ii) construct closed form expressions for complete life expectancy using the properties of the special functions as applicable in classical mortality dynamics. To circumvent the need for any rigorous numerical procedures, the advanced technique of the Gradshteyn and Ryzhik’s analytic integral is applied in computing the complete life expectancies. From our results, it is apparent that ex(male)< ex(female). Specifically, within the interval 111<x<119 for women, there is a sharp decrease in complete life expectancies whereas for men within the interval 75<x<119, life expectancies sharply decrease confirming earlier exposure of men to mortality risk.
Downloads
References
Pflaumer, P. (2011). Methods of estimating selected life table parameters using Gompertz distribution. Conference: JSM Proceedings, Social Statistics Section, Alexandria, 733-747.
Palo, C.D. (2023). On a closed form expression and its approximation to Gompertz life dsparity. Demographic Research, 49(1), 1-12. https://doi.org/10.4054/DemRes.2023.49.1
Missov M.I.., and Lennart, L.A. (2013). Gompertz-Makeham life expectancies: Expressions and applications. Theoretical Population Biology, 90, 29-35. http://dx.doi.org/10.1016/j.tpb.2013.09.013
Kulinskaya E., Gitsels L.A., Bakbergenuly, Wright N.R. (2020). Calculation of changes in life expectancy based on proportional hazards model of an intervention. Insurance: Mathematics and Economics 93, 97-33.
Cohen J. (2010). Life expectancy is the death-weighted average of the reciprocal of the survival-specific force of mortality. Demographic Research, 22(5), 115-128. https://doi.org/10.4054/DemRes.2010.22.5
Dragan, M. (2022). Some general Gompertz and Gompertz-Makeham life expectancy models. Sciendo, 30(3), 117-142. https://doi.org/10.2478/auom-2022-0037
Jameson G. (2016). The incomplete gamma functions. The Mathematical Gazette 100(548), 298-306. https://doi.org/10.1017/mag.2016.67
Neil, A. Life contingencies. The Institute of Actuaries and Faculty of Actuaries, (1979) special edition.
Forfar D., McCutcheon J., and Wilkie D. (1988). On graduation by mathematical formula. Journal of the Institute of Actuaries, 115, 1-135
Siswono, G.O., Azmi, U., and Syaifudin W.H. (2021). Mortality projection on Indonesia’s abridged life table to determine the EPV of term annuity. Jurnal Varian 4(2), 159-168. https://doi.org/10.30812/varian.v412.1094
Debon, A., Montes, F., and Sala, R. A. (2005). Comparison of parametric models for mortality graduation. Application to mortality data for the Valencia Region (Spain). Sort. 29(2), 269-288
Walters H.R., and Wilkie A.D. (1987). A short note on the construction of life tables and multiple decrement tables. Journal Institute of Actuaries, 114, 569-580.
Castro-Perez, J., Aguilar-Sanchez G.P., and Gonzalez-Nucamendi A. (2020). Approximate integration through remarkable points using the intermediate value theorem. Scientia et Technica Ano XXV, 25(1), 142-149.
Chowdhury M. A. (2012). Brief study on Gompertz-Makeham model and some aspects on agricultural growth of Assam. International Journal of Mathematical Archive, 3(6).
Kara E.K. A. (2021). Study on modelling of lifetime with right-truncated composite lognormal Pareto distribution: Actuarial premium calculations. Gazi University Journal of Science. 34(1), 272-288, https://doi.org/10.35378/gujs.646899
Gradshteyn I.S., and Ryzhik I.M. (2007). Table of integrals, series and products. Academic Press, New York.
Ogungbenle G.M., Ihedioha, S.A., and Ogungbenle O.G. (2023). The Gradshteyn and Ryzhik’s integral and the theoretical computation of involving the continuous whole life annuities. Nepal Journal of Mathematical Sciences, 4(2), 17-30.
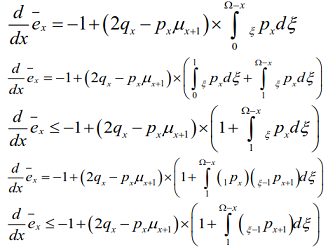
Downloads
Published
Issue
Section
License
Copyright (c) 2024 Lafia Journal of Scientific and Industrial Research

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.









