Mathematical Modeling of the Spread of the Ebola Virus Disease
DOI:
https://doi.org/10.62050/fjst2024.v8n2.566Keywords:
Difference equation method, Ebola, Mathematical modeling, Reproduction numberAbstract
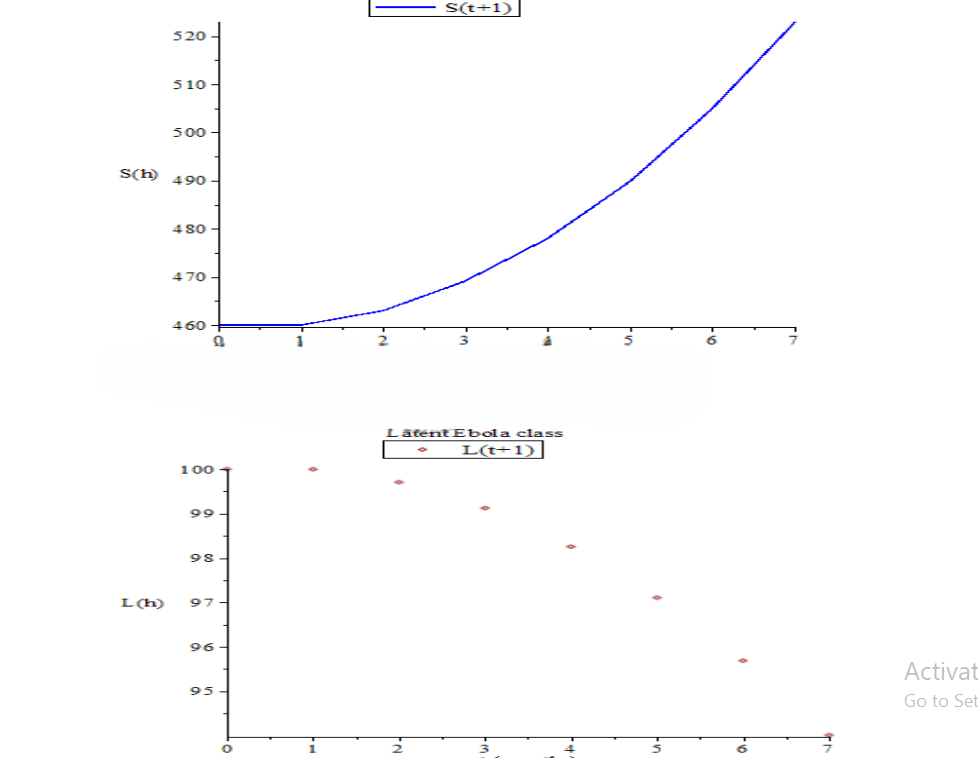
Ebola, a viral and fatal disease with occasional outbreaks on the continent of Africa affects mostly humans and non-human primates, and poses a great health challenge to this part of the globe. The transmission of Ebola Virus can be through direct contact with blood, bodily fluids, or skin of Ebola Virus Disease patients or those who have passed away from the illness. In this paper, we formulate a mathematical model of the transmission of the Ebola virus disease in a population capturing its dynamics to study the impact of healthcare policies on its spread. The model is a four compartment model consisting of Susceptible, Latent, Infectious and Recovery compartments. To gain a good understanding of the model, the formulated model is transformed into difference equations. The basic
reproduction number R0 is derived using the next generation matrix method. Further, the disease-free equilibrium of the model is obtained and its stability analysis is carried out. The result shows that the disease-free equilibrium point is locally stable if R0 < 1 but may not be asymptotically stable, indicating that the disease will eventually die out. Conversely, if R0 > 1, an endemic equilibrium exists, and the disease will persist at a stable level. Numerical simulations obtained illustrate the efforts of the parameters on the compartment of the model.
Downloads
References
Amira, R. and Delfim, F. M. (2015). Mathematical Modeling, Simulation and Optimal Control of the Ebola Outbreak in West Africa. Discrete Dynamics in Nature and Society. 842792, 9. https://doi.org/10.11555/2015/842792.
Berge, T., Lubuma, J. M., Moremedi, G. M., and Morris, N. (2017). A Simple Mathematical Model for Ebola in Africa. 3758. https://doi.org/10.1080/17513758.2016.1229817.
Chretien, J. P., Riley, S. and George, D. B. (2015). Mathematical Modeling of the West Africa Ebola Epidemic. ELife. 2015, 1–15. https://doi.org/10.7554/eLife.09186.
Diane, S. N (2019). Mathematical Models of Ebola Virus Disease with Socio-economic Dynamics (Doctoral dissertation, Stellenbosch University). Retrieved from http:scholar.sun.ac.za.
Diane, S., Njankou, D. and Nyabadza, F. (2017). Modelling the Potential Role of Media Campaigns in Ebola Transmission Dynamics. Hindawi International Journal of Differential Equation. 2017 (3758269), 13. http://doi.org/10.1155/2017/3758269.
Jiang, S., Wang, K., Li, C., Hong, G., Zhang, X., Shan, M., Li, H., & Wang, J. (2017). Mathematical Models for Devising the Optimal Ebola Virus Disease Eradication. Journal of Translational Medicine, 15(1), 1–10. https://doi.org/10.1186/s12967-017-1224-6.
Li, L., Du, L. X., Yan, Z., Zhang, J. and Wu, Y. P. (2020). No Title. A Method for Parameters Estimation in a Dynamical Model of Ebola Virus Transmission in Sierra Leone. Hindawi Publishing Corporation, Complexity, 2020. https://doi.org/https://doi.org/10.1155/2020/9172835.
Li, Z. (2016). The Spread of Ebola Virus Based On SEIHCR Model. Emcpe, 254–257.
Mhlanga, A. (2019). Dynamical Analysis and Control Strategies in Modelling Ebola Virus Disease. Adv Differ Equ. https://doi.org/10.1186/s13662-019-2392-x.
Nazir, A., Ahmed, N., Khan, U., Mohyud-din, S. T., Sooppy, K., and Khan, I. (2020). An Advanced Version of a Conformable Mathematical Model of Ebola Virus Disease in Africa. Alexandria Engineering Journal, 59(5), 3261–3268. https://doi.org/10.1016/j.aej.2020.08.050.
Ngwa, G. A., and Teboh-ewungkem, M. I. (2016). A Mathematical Model with Quarantine States for the Dynamics of Ebola Virus Disease in Human Populations. Computational and Mathematical Mehods in Medicine. 2016. https://doi.org/10.1155/2016/9352725.
Olajide, A. J. (2020). Mathematical Analysis of the Role of Detection Rate on Dynamical Spread of Ebola Virus Disease. Journal of Modeling and Simulation of Materials. 3(1), 37–52. https://doi.org/10.21467/jmsm.3.1.37-52.
Osemwinyen, C. A. (2015). Mathematical Modelling of the Transmission Dynamics of Ebola Virus. Applied and Computational Mathematics, 4(4), 313. https://doi.org/10.11648/j.acm.20150404.19.
Rachah, A., and Saidi, M. (2021). Mathematical Modeling and Optimal Control of Ebola Virus Transmission Dynamics, International Journal of Applied Mathematics. 34(3), 535–554. https://doi.org/10.12732/ijam.v34i3.9.
Rachah, A., & Torres, D. F. M. (2015). Mathematical Modelling, Simulation, and Optimal Control of the 2014 Ebola Outbreak in West Africa. Hindawi Publishing Corporation, Discrete Dynamics in Nature and Society, 2015(842792), 9. https://doi.org/http://dx.doi.org/10.1155/2015/842792
Tae, S. A., & Young, S. A. (2015). Modeling the Spread of Ebola. Osong Public Health Res perspect. 2016(7) 43-48. http://dx.doi.org/10.1016/j.phrp.2015.12.012.