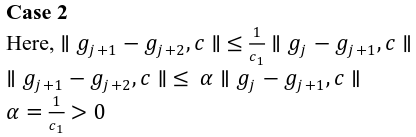Existence and Uniqueness of a Second Order Difference Equation of Accretive Type in 2-Banach Spaces

Gabriel Gyegwe; I. G. Bassi

doi:10.62050/fjst2024.v8n1.231

Authors

Gabriel Gyegwe Department of Mathematics, Federal University of Lafia Author
Bassi I. G. Department of Mathematics, Federal University of Lafia Author

DOI:

https://doi.org/10.62050/fjst2024.v8n1.231

Keywords:

Accretive operator, m-accretive operator, 2-normed space, 2-Banach space , expansive mappings

Abstract

In this paper, we investigate the existence and uniqueness of solutions to a homogeneous second order difference inclusion of accretive type in 2-Banach spaces using expansive mappings and 2-Banach contraction mapping.

Downloads

Download data is not yet available.

References

Apreutessei, N. C. (2003). Existence and Asymptotic Behaviour for Some Difference Equations Associated with Accretive Operators. In: Vioeri Barbu, et al. (Eds), Analysis and Optimization of Differential Systems, IFIP International

Federation for Information Processing. https://doi.org/10.1007/978-387-35690-7_44

Barbu, V. (1976). Nonlinear Semi groups and Differential Equations in Banach Spaces. Noordhoff International Publishing, Leiden.

Barbu, V. (2010). Nonlinear Differential Equations of Monotone Types in Banach Spaces. Springer Monographs. https://doi.org/10.1007/978-1-4419-5542-5

Chouha, P. and Malviya, N. (2013). Fixed points of expansive type mapping in 2-Banach spaces. Int. J. of Analysis and Applications, 3(1), 60-67. http://www.etamaths.com

Das, D., Goswami, N. and Mishra, V. N. (2017). Some fixed point theorems in the projective tensor product of 2-Banach spaces. Global Journal of Advanced Research on Classical and Modern Geometrics, 6(1), 20-36.

Eskandani, G. Z. and Rassians, J. M. (2016). Approximation of general ???? −cubic functional equations in 2-Banach spaces. YKP. Mam. ⊃ +⊂ypH, 68(10), 1027-3190.

Gurdal, M. and Savas, E. (2021). A note on uniquely remotal set in 2-Banach spaces. Electronic J. of Mathem. Analysis and Application, 9(2), 151-157. https://maths-frac.org/Journal/EJMAA

Gyegwe, G. T. and Bassi, I. G. (2024). On the existence and uniqueness of solutions to a non-homogeneous second order difference equation of accretive type of 2-Banach spaces. International Journal of Mathematics and Computer Research (IJMCR), 12(1), 4051-4054. https://doi.org/10.47191/jmcr/v12i2.07

Harikrishnan, P. K. and Ravindran, K. T. (2011). Some properties of accretive operators in linear 2-Normed spaces. International Mathematical Forum, 6(59), 2941-2947.

Harikrishnan, P., Guillen, B. L., Agawral, R. P. and Moradi, H. R. (1986). Strong AHD weak convergence in 2-robailistic normed spaces. Advances in the Theory of Nonlinear Analysis and its Applications, 5(4), 454-466. https://doi.org/10.1031197/atnaa.921900

Kabbaj, R. E. S. (2020). 2-2Banach stability results for radical cubic functional equation related to quadratic mapping. J. of Linear and Topological Algebra, 09(1), 35-51. http://jlta.iaucth.ac.ir

Khatibzadeh, H. (2012). Convergence of solutions to a second-order difference inclusion. Nonlinear Analysis, 75, 3503-3509. https://doi.org/10.1016/j.na.2012.01.010

Kir, M. (2013). A new approach to the accretive operators arising from 2-Banach spaces. General Math Notes, 16(2), 48-54. http://www.geman.in

Kumar, D. R. and Pitchaimani, M. (2019). Approximation of common fixed point in 2-Banach spaces with applications. Applied General Topology, 20(1), 43-55

Lakshmikanthan, V. and Trigiante, D. (2003). Theory of Difference Equations-Numerical method and Applications, 2nd ed. Bulletin (New Series) of the American Mathematical Society, 40(2), 259-262

Morasanu, G. (1988). Nonlinear Evolution Equations and Applications. Editura Academiei Romane (D. Reidei Publishing Company), Bucharest

Pilakkat, R. and Thirumangalath, S. (2021). Results in linear 2Normed spaces analogous to Baire’s theorem and closed graph theorem. International Journal of Pure and Applied Mathematics, 74(4), 509-517, 2012

Poffald, E. I. and Reich, S. (1986). An incomplete cauchy problem. Journal of Mathematical Analysis and Applications, 113, 514-543

Rouhani, B. D. and Khatibzadeh, H. (2012). Existence and asymptotic behaviour of solutions to first and second-order difference equations with periodic forcing. Journal of Difference Equations and Application, 18(9), 1593-1606. http://www.tandfonline.com/loi/gdea20

Rouhani, B. D., Jamshidnezhad, P. J. and Saeidi, S. (2019). Zeros of accretive operators and asymptotics of a second-order differense inclusion in Banach spaces. J. Math. Anal. 480, 123428. https://doi.org/10.1016/j.jmaa.2019.123428

Saha, M., Dey, D., Ganguly, A. and Debnath, L. (2012). Asymptotic regularity and fixed point theorems on a 2-2Banach spaces. Surveys in Math. and its Applic., 7, 31-38. http://utgjiu.ro/math/sma

Sari, C. K. (2015). Some properties of m-accretive operators in Normed spaces. International Conference on Science, Technology and Humanity, 2477-3328